Forbidden subposets for fractional weak discrepancy at most k
2009/8/28 Friday 4PM-5PM
The fractional weak discrepancy of a poset (partially ordered set) P, written wd(P), is the least k such that some 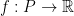 satisfies f(y)-f(x)≤1 for
satisfies f(y)-f(x)≤1 for  and |f(y)-f(x)|≤k for x|y. Minimal forbidden subposets are often called obstructions. Shuchat, Shull, and Trenk determined the obstructions for the property wd(P)<1: the obstructions are 2+2 and 3+1. We determine the obstructions for the property wd(P)≤k when k is an integer. In this talk, the complete collection of the obstructions for wd(P)≤k for each k≥2 – which is an infinite set – will be discussed.
and |f(y)-f(x)|≤k for x|y. Minimal forbidden subposets are often called obstructions. Shuchat, Shull, and Trenk determined the obstructions for the property wd(P)<1: the obstructions are 2+2 and 3+1. We determine the obstructions for the property wd(P)≤k when k is an integer. In this talk, the complete collection of the obstructions for wd(P)≤k for each k≥2 – which is an infinite set – will be discussed.
This is joint work with Douglas B. West.