The topology of restricted partition posets
JiYoon Jung
NIMS
NIMS
2014/11/04 Tuesday 4PM-5PM
Room 1409
Room 1409
For each composition 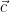 we show that the order complex of the poset of pointed set partitions
we show that the order complex of the poset of pointed set partitions  is a wedge of spheres of the same dimension with the multiplicity given by the number of permutations with descent composition
is a wedge of spheres of the same dimension with the multiplicity given by the number of permutations with descent composition 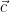 . Furthermore, the action of the symmetric group on the top homology is isomorphic to the Specht module
. Furthermore, the action of the symmetric group on the top homology is isomorphic to the Specht module  where
where 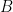 is a border strip associated to the composition. We also study the filter of pointed set partitions generated by a knapsack integer partition and show the analogous results on homotopy type and action on the top homology.
is a border strip associated to the composition. We also study the filter of pointed set partitions generated by a knapsack integer partition and show the analogous results on homotopy type and action on the top homology.