Dept. of Mathematical Sciences, KAIST, Korea.
Archive for the ‘2008’ Category
Jang Soo Kim (김장수), A combinatorial approach to the power of 2 in the number of involutions
Friday, December 5th, 2008Dept. of Mathematical Sciences, KAIST, Korea.
Yoomi Rho (노유미), Turán type problems forbidding complete graphs and complete multipartite graphs together
Monday, November 10th, 2008Dept. of Mathematics, Univ. of Incheon, Incheon, Korea.
Let t and n be positive integers with n≥t≥2. Determine the maximum number of edges of a graph of order n that contains neither Kt nor Kt,t as a subgraph.
They also solved this problem when n=2t. Obviously when n<2t, the problem reduces to Turán's problem which forbids only Kt. We solve the problem when n=2t+1. We raise a problem which forbids Kt and Kt,n-t together and a problem which forbids Kt and Kt,t,t together.
Sung-Pil Hong (홍성필), Approximability of a batch consolidation problem
Tuesday, October 28th, 2008Dept. of Industrial Engineering, Seoul National University, Seoul, Korea.
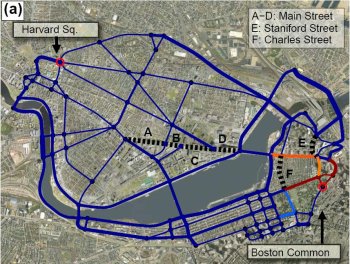
Hawoong Jeong (정하웅), Price of Anarchy in Transportation Networks
Friday, October 17th, 2008Dept. of Physics, KAIST, Daejeon, Korea.
Uncoordinated individuals in human society pursuing their personally optimal strategies do not always achieve the social optimum, the most beneficial state to the society as a whole. Instead, strategies form Nash equilibria, which are, in general, socially suboptimal. Society, therefore, has to pay a price of anarchy for the lack of coordination among its members, which is often difficult to quantify in engineering, economics and policymaking. Here, we report on an assessment of this price of anarchy by analyzing the road networks of Boston, New York, and London as well as complex model networks, where one’s travel time serves as the relevant cost to be minimized. Our simulation shows that uncoordinated drivers possibly spend up to 30% more time than they would in socially optimal traffic, which leaves substantial room for improvement. Counterintuitively, simply blocking certain streets can partially improve the traffic condition to a measurable extent based on our result.
One-sentence summaries: Traffic in transportation networks – often substantially suboptimal due to a lack of coordination among users – can be guided to the social optimum without directly controlling individual behavior by adjusting the underlying network structure appropriately.
Andreas Holmsen, Points surrounding the origin
Monday, August 25th, 2008Div. of Computer Science, KAIST, Daejeon, Korea.
Many problems in discrete and computational geometry can be reduced to combinatorial questions concerning systems of segments or triangles in the plane. In spite of what (little) we can say about these planar questions, much less is known in higher dimensions. In this talk we will survey some of these questions and classical results, and present the following theorem: Let d>2 and n>d+1 and P a set of n points in d-dimensional Euclidean space. Then P contains a subset Q of d points such that for any point p in P, the simplex spanned by Q and p does not contain the origin in its interior. This answers a question by R.Strausz, and along the way we strengthen the Colored Helly and Caratheodory theorems, due to L. Lovász and I. Bárány, respectively.
Joint work with János Pach and Helge Tverberg.