Some Advances in Sidorenko’s Conjecture
Joonkyung Lee
University of Oxford, UK
University of Oxford, UK
2014/09/04 *Thursday* 4PM-5PM
Room 1409
Room 1409
Sidorenko’s conjecture states that for every bipartite graph 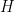 on
on 
\begin{eqnarray*}
\int \prod_{(i,j)\in E(H)} h(x_i, y_j) d\mu^{|V(H)|}
\ge \left( \int h(x,y) \,d\mu^2 \right)^{|E(H)|}
\end{eqnarray*}
holds, where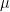 is the Lebesgue measure on
is the Lebesgue measure on ![[0,1] [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0) and
and 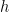 is a bounded, non-negative, symmetric, measurable function on
is a bounded, non-negative, symmetric, measurable function on ![[0,1]^2 [0,1]^2](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E2&bg=ffffff&fg=000000&s=0) . An equivalent discrete form of the conjecture is that the number of homomorphisms from a bipartite graph
. An equivalent discrete form of the conjecture is that the number of homomorphisms from a bipartite graph 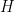 to a graph
to a graph 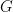 is asymptotically at least the expected number of homomorphisms from
is asymptotically at least the expected number of homomorphisms from 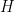 to the Erdos-Renyi random graph with the same expected edge density as
to the Erdos-Renyi random graph with the same expected edge density as 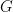 . In this talk, we will give an overview on known results and new approaches to attack Sidorenko’s conjecture.
. In this talk, we will give an overview on known results and new approaches to attack Sidorenko’s conjecture.
This is a joint work with Jeong Han Kim and Choongbum Lee.
\begin{eqnarray*}
\int \prod_{(i,j)\in E(H)} h(x_i, y_j) d\mu^{|V(H)|}
\ge \left( \int h(x,y) \,d\mu^2 \right)^{|E(H)|}
\end{eqnarray*}
holds, where
This is a joint work with Jeong Han Kim and Choongbum Lee.