KAIST Graph Theory Day 2011
2011/5/10 Tuesday (Room: 1501, Building E6-1)
Poster (KAIST Graph Theory Day)
Registration
List of speakers
- 11AM-12PM Maria Chudnovsky (Columbia University, USA) : Coloring some perfect graphs
- 2PM-3PM Ken-ichi Kawarabayashi (NII, Japan) : A separator theorem in minor-closed class of graphs
- 4PM-5PM Bojan Mohar (SFU, Canada) : On the chromatic number of digraphs
- 5PM-6PM Paul Seymour (Princeton University, USA) : Colouring Tournaments
Coloring some perfect graphs
Maria Chudnovsky
A graph G is called perfect if for every induced subgraph H of G, the chromatic number and the clique number of H are equal. After the recent proof of the Strong Perfect Graph Theorem, and the discovery of a polynomial-time recognition algorithm, the central remaining open question about perfect graphs is finding a combinatorial polynomial-time coloring algorithm. (There is a polynomial-time algorithm known, using the ellipsoid method). Recently, we were able to find such an algorithm for a certain class of perfect graphs, that includes all perfect graphs admitting no balanced skew-partition. The algorithm is based on finding special “extremal” decompositions in such graphs; we also use the idea of “trigraphs”.
This is joint work with Nicolas Trotignon, Theophile Trunck and Kristina Vuskovic.
A separator theorem in minor-closed class of graphs
Ken-ichi Kawarabayashi
It is shown that for each t, there is a separator of size
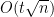
in any n-vertex graph G with no K
t-minor.
This settles a conjecture of Alon, Seymour and Thomas (J. Amer. Math. Soc., 1990 and STOC’90), and generalizes a result of Djidjev (1981), and Gilbert, Hutchinson and Tarjan (J. Algorithm, 1984), independently, who proved that every graph with n vertices and genus g has a separator of order

, because K
t has genus Ω(t
2).
Joint work with Bruce Reed.
On the chromatic number of digraphs
Bojan Mohar
Several reasons will be presented why the natural extension of the notion of undirected graph colorings is to partition the vertex set of a digraph into acyclic sets. Additionally, some recent results in this area, the proofs of which use probabilistic techniques, will be outlined.
Colouring Tournaments
Paul Seymour
A tournament is a digraph obtained from a complete graph by directing its edges, and colouring a tournament means partitioning its vertex set into acyclic subsets (acyclic means the subdigraph induced on the subset has no directed cycles). This concept is quite like that for graph-colouring, but different. For instance, there are some tournaments H such that every tournament not containing H as a subdigraph has bounded chromatic number. We call them heroes; for example, all tournaments with at most four vertices are heroes.
It turns out to be a fun problem to figure out exactly which tournaments are heroes. We have recently managed to do this, in joint work with Berger, Choromanski, Chudnovsky, Fox, Loebl, Scott and Thomassé, and this talk is about the solution.