Research Interest
Biochemical Network Detection with Oscillating Timecourse Data
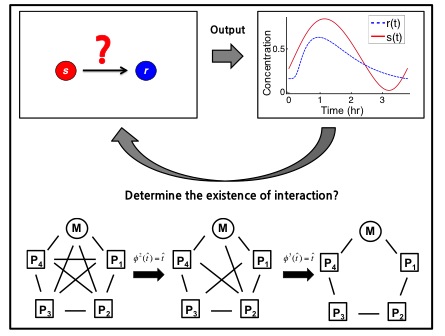 If we can accurately record the oscillating timecourses of genes and proteins in a cellular clock, what can we infer about the biochemical network generating the rhythms? I formulated this question as an existence and uniqueness problem and proved that the network interactions, and even biochemical rates, can sometimes uniquely be determined from only gene and protein timecourses. This theory provides a simple algorithm to determine whether two given species have a biochemical interaction. Using this algorithm to identify pairs of unrelated species, I was able to reveal the biochemical network of various biological oscillator models (e.g. the extended Goodwin oscillator) from their timecourse data. Currently, I am trying to apply this algorithm to real experimental data.
If we can accurately record the oscillating timecourses of genes and proteins in a cellular clock, what can we infer about the biochemical network generating the rhythms? I formulated this question as an existence and uniqueness problem and proved that the network interactions, and even biochemical rates, can sometimes uniquely be determined from only gene and protein timecourses. This theory provides a simple algorithm to determine whether two given species have a biochemical interaction. Using this algorithm to identify pairs of unrelated species, I was able to reveal the biochemical network of various biological oscillator models (e.g. the extended Goodwin oscillator) from their timecourse data. Currently, I am trying to apply this algorithm to real experimental data.
Kim JK and Forger DB, On the Existence and Uniqueness of Biological Clock Models Matching Experimental Data, SIAM J. APPL. MATH., 72 (2012), pp. 1842-1855 (Reported at Vertical News) PDF
Quasi-steady State Approximtions in Stochastic Simulations
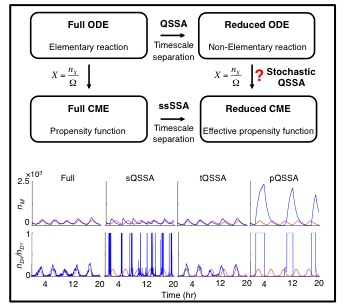 If timescales of biochemical network reactions are disparate, can we use quasi-steady state approximation (QSSA) in stochastic simulations similar to deterministic simulations? That is, can we use non-elementary reaction rate functions (e.g. Hill functions) to derive the propensity functions in Gillespie algorithms? Many previous studeis used the stochastic QSSA with the beleif that the stochastic QSSA is accurate as long as the deterministic QSSA is accurate. However, I found that this is not true. That is, I proved that, unlike the deterministic QSSA, the validity of the stochastic QSSA does not follow from timescale separation alone, but also depends on the sensitivity of the non-elementary reaction functions to changes in the slow species. Specifically, the stochastic QSSA becomes more accurate when this sensitivity is small. Different types of QSSAs result in non-elementary functions with different sensitivities, with the total QSSA producing less sensitive functions than standard or pre-factor QSSA. We prove that, as a result, the stochastic QSSA becomes more accurate when non-elementary reaction functions are obtained using the total QSSA.
If timescales of biochemical network reactions are disparate, can we use quasi-steady state approximation (QSSA) in stochastic simulations similar to deterministic simulations? That is, can we use non-elementary reaction rate functions (e.g. Hill functions) to derive the propensity functions in Gillespie algorithms? Many previous studeis used the stochastic QSSA with the beleif that the stochastic QSSA is accurate as long as the deterministic QSSA is accurate. However, I found that this is not true. That is, I proved that, unlike the deterministic QSSA, the validity of the stochastic QSSA does not follow from timescale separation alone, but also depends on the sensitivity of the non-elementary reaction functions to changes in the slow species. Specifically, the stochastic QSSA becomes more accurate when this sensitivity is small. Different types of QSSAs result in non-elementary functions with different sensitivities, with the total QSSA producing less sensitive functions than standard or pre-factor QSSA. We prove that, as a result, the stochastic QSSA becomes more accurate when non-elementary reaction functions are obtained using the total QSSA.
Kim JK, Josic K, and Bennett MR, The validity of quasi steady-state approximations in discrete stochastic simulations, Biophysical Journal 107 (2014) PDF
Kim JK, Josic K, and Bennett MR, The relationship between deterministic and stochastic quasisteady state approximation, BMC Systems Biology 9:87(2015) PDF
Period Regulation Mechanisms for Circadian Rhythms
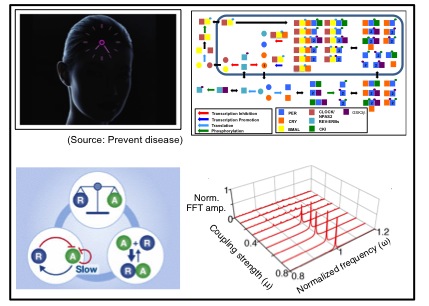 Circadian rhythms are 24-hour periodic rhythms that time daily events through the body. How do cells generate rhythms with a constant period over a wide range of environmental conditions? To understand mechanisms of circadian clocks systemically, I developed the most detailed and accurate mathematical model of this system to date by piecing together data from various experimental studies. Through simulation and analysis, I found that the mammalian circadian clocks have interesting mechanisms for regulating their periods in response to transcription rate changes, temperature changes and the presence of coupling signal. These mechanisms have been experimental validated by David Virshup lab and Choogon Lee lab. Furthemore, collaboration with Pfizer company, our mathematical model of the mammalian circadian clocks has been used to test the drug effect on the circadian phase.
Circadian rhythms are 24-hour periodic rhythms that time daily events through the body. How do cells generate rhythms with a constant period over a wide range of environmental conditions? To understand mechanisms of circadian clocks systemically, I developed the most detailed and accurate mathematical model of this system to date by piecing together data from various experimental studies. Through simulation and analysis, I found that the mammalian circadian clocks have interesting mechanisms for regulating their periods in response to transcription rate changes, temperature changes and the presence of coupling signal. These mechanisms have been experimental validated by David Virshup lab and Choogon Lee lab. Furthemore, collaboration with Pfizer company, our mathematical model of the mammalian circadian clocks has been used to test the drug effect on the circadian phase.
- Kim JK, Protein sequestration versus Hill-type repression in circadian clock models, IET Systems Biology 10(4) 125-135 (2016) PDF
- DAlessandro M, Beesley S, Kim JK, Chen R, Abich E, Cheng W, Yi P, Takahashi JS, Lee C, A tunable artificial circadian clock in clock-defective mice, Nature Communication 6:9587 (2015) PDF
- Zhou M*, Kim JK*, Ling Eng GW, Forger DB, Virshup DM, A Period2 Phosphoswitch Regulates and Compensates Circadian Period (*1st co-author), Molecular Cell 60 (2015) (Reported at Science Daily, MBC & YTN) PDF
- Ye C*, Kim JK*, Hirning A, Josic K, and Bennett MR, Emergent genetic oscillations in a synthetic microbial consortium (*1st co-author), Science 349.6251 (2015) (Reported at Science Daily & YTN) PDF
- Kim JK, Kilpatrick Z, Bennett MR, and Josic K, Molecular mechanisms that regulate the coupled period of the mammalian circadian clock, Biophysical Journal 106 (2014) (Featured article of journal) PDF
- Goriki A, Hatanaka F, Myung J, Kim JK, Yoritaka T, Tanoue S, Abe T, Kiyonari H, Fujimoto K, Kato Y, Matsubara A, Forger DB, and Takumi T. A novel protein, CHRONO, functions as a core component of the mammalian circadian clock, PLoS Biology 12 (2014) (Reported at Gene News and Science Daily) PDF
- Kim JK, Forger DB, Marconi M, Wood D, Doran A, Wager TT, Chang C and Walton K, Modeling and Validating Chronic Pharmacological Manipulation of Circadian Rhythms, Nature CPT:Pharmacometrics & Systems Pharmacology 8 (2013) PDF
- Kim JK and Forger DB, A Mechanism for Robust Circadian Timekeeping via stoichiometric balance, Nature/EMBO Molecular Systems Biology 8, (2012) (Recommended by F1000 Prime) PDF
- Zhou M*, Kim JK*, Ling Eng GW, Forger DB, Virshup DM, A Period2 Phosphoswitch Regulates and Compensates Circadian Period (Under reivew, * Equally contributed)
DNA Damage Induced-p53 Rhythms
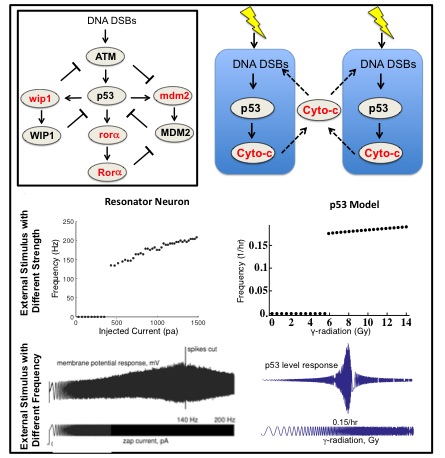 p53 is one of the most important tumor suppressors. p53 rhythms occur in response to external stimuli such as DNA damage. Neurons, one of the most widely studied biological oscillators, also can generate rhythms when external stimuli (currents) are given. In my work to develop a new mathematical model for p53 rhythms, I found that DNA damaged cells behave like type II neurons, which act as resonators. The fact that type II neurons easily synchronize their rhythms when they are coupled led to the question of whether neighboring cells also have a coupling mechanisms to synchronize p53 rhythms. Interestingly, a recent experimental study found a potential coupling signal (Cytochrom-c) among neighboring cells after DNA damage. Moreover, when I induced stochasticity into the model through the Gillespie algorithm, the coupling significantly reduced the variation in the period of p53 rhythms, which is essential to prevent tumorigenesis. Furthermore, it is known that the disruption of circadian clocks due to mutation or shift work increase the risk of getting cancer. However, the molecular pathway for this relationship between circadian clock and cancer has not been known. Recently, we found that p53 interacts with Per2 protein (one of core circadian clock components) in collaboration with Carla Finkielstein lab and John Tyson lab at Virginia Tech. Now, we explore how this interaction between p53 and Per2 plays role in regulating DNA damage with the combination of mathematical model and experiments.
p53 is one of the most important tumor suppressors. p53 rhythms occur in response to external stimuli such as DNA damage. Neurons, one of the most widely studied biological oscillators, also can generate rhythms when external stimuli (currents) are given. In my work to develop a new mathematical model for p53 rhythms, I found that DNA damaged cells behave like type II neurons, which act as resonators. The fact that type II neurons easily synchronize their rhythms when they are coupled led to the question of whether neighboring cells also have a coupling mechanisms to synchronize p53 rhythms. Interestingly, a recent experimental study found a potential coupling signal (Cytochrom-c) among neighboring cells after DNA damage. Moreover, when I induced stochasticity into the model through the Gillespie algorithm, the coupling significantly reduced the variation in the period of p53 rhythms, which is essential to prevent tumorigenesis. Furthermore, it is known that the disruption of circadian clocks due to mutation or shift work increase the risk of getting cancer. However, the molecular pathway for this relationship between circadian clock and cancer has not been known. Recently, we found that p53 interacts with Per2 protein (one of core circadian clock components) in collaboration with Carla Finkielstein lab and John Tyson lab at Virginia Tech. Now, we explore how this interaction between p53 and Per2 plays role in regulating DNA damage with the combination of mathematical model and experiments.
Gotoh T*, Kim JK*†, Liu J, Vila-Caballera M, Stauffera PE, Tyson JJ, Finkielstein C†, Model-driven experimental approach reveals the complex regulatory distribution of p53 by the circadian factor Period 2, PNAS 113(47) 13516-13521(2016) (*1st co-author †co- corresponding author) PDF (Reprted at Asian Scientist & YTN).
Kim JK and Jackson T, Mechanisms for Enhancing Sustainability of p53 pulses, PLoS ONE 8, (2013) PDF
