Month: November 2021

Our second KMGS will be held on November 25th, Thursday, via Zoom and Gather Town.
We invite Wooyoung Chin from Dept. of Mathematical Sciences, KAIST and Donggyu Kim from Dept. of Mathematical Sciences, KAIST and IBS Discrete Mathematics Group (DIMAG).
The abstracts of two talks are as follows.

1st slot (PM 12:00~12:20)
Speaker: Wooyoung Chin (진우영) from Dept. of Mathematical Sciences, KAIST, supervised by Prof. Paul Jung (폴 정 교수님)
Title: A new elementary proof of the central limit theorem
Discipline: Probability
Abstract: The proof of the central limit theorem (CLT) is often deferred to a graduate course in probability because the notion of characteristic functions is sometimes considered too advanced. I’ll start the talk by reviewing the past efforts to provide an elementary proof of the CLT which is not based on characteristic functions. Then I will explain a new proof of the CLT that derives it from the de Moivre-Laplace theorem, which is the CLT for Bernoulli random variables. The de Moivre-Laplace theorem is the first instance of the CLT in the history, and can be proved directly by computation.
Language: Korean (English if it is requested)

2nd slot (PM: 12:25~12:45)
Speaker: Donggyu Kim (김동규) from Dept. of Mathematical Sciences, KAIST and IBS Discrete Mathematics Group (DIMAG), supervised by Prof. Sang-il Oum (엄상일 교수님)
Title: Eigenvalues and parity factors in graphs
Discipline: Graph Theory
Abstract: Let $G$ be a graph and let $g, f$ be nonnegative integer-valued functions defined on $V(G)$ such that $g(v) \le f(v)$ and $g(v) \equiv f(v) \pmod{2}$ for all $v \in V(G)$.A $(g,f)$-parity factor of $G$ is a spanning subgraph $H$ such that for each vertex $v \in V(G)$, $g(v) \le d_H(v) \le f(v)$ and $f(v)\equiv d_H(v) \pmod{2}$.In this paper, we prove sharp upper bounds for certain eigenvalues in an $h$-edge-connected graph $G$ with given minimum degree to guarantee the existence of a $(g,f)$-parity factor; we provide graphs showing that the bounds are optimal. This is a joint work with Suil O.
Language: Korean (English if it is requested)

We are glad to inform you that our first KMGS will start on November 18th, Thursday, via Zoom and Gather Town.
We invite Ho-Youn Kim from Dept. of Mathematical Sciences, KAIST and Doyoung Choi from Dept. of Mathematical Sciences, KAIST and IBS Center for Complex Geometry (CCG).
The abstracts of two talks are as follows.

1st slot (PM 12:00~12:20)
Speaker: Ho-youn Kim (김호연) from Dept. of Mathematical Sciences, KAIST, supervised by Prof. Yong Jung Kim (김용정 교수님)
Title: What is the correct diffusion equation in heterogeneous mediums
Discipline: PDE
Abstract: In the classical diffusion theory, the diffusivity has been regarded as an intrinsic property of particles. However, it can’t explain diffusion phenomena in heterogeneous medium, one of the most famous example is Soret effect. The diffusivity can be changed along different mediums and it arises a question: how can we express heterogeneous diffusion. In this talk, I’ll introduce the heterogeneous diffusion equation we found and give some experimental data verifying this work.
Language: Korean

2nd slot (PM 12:25~12:45)
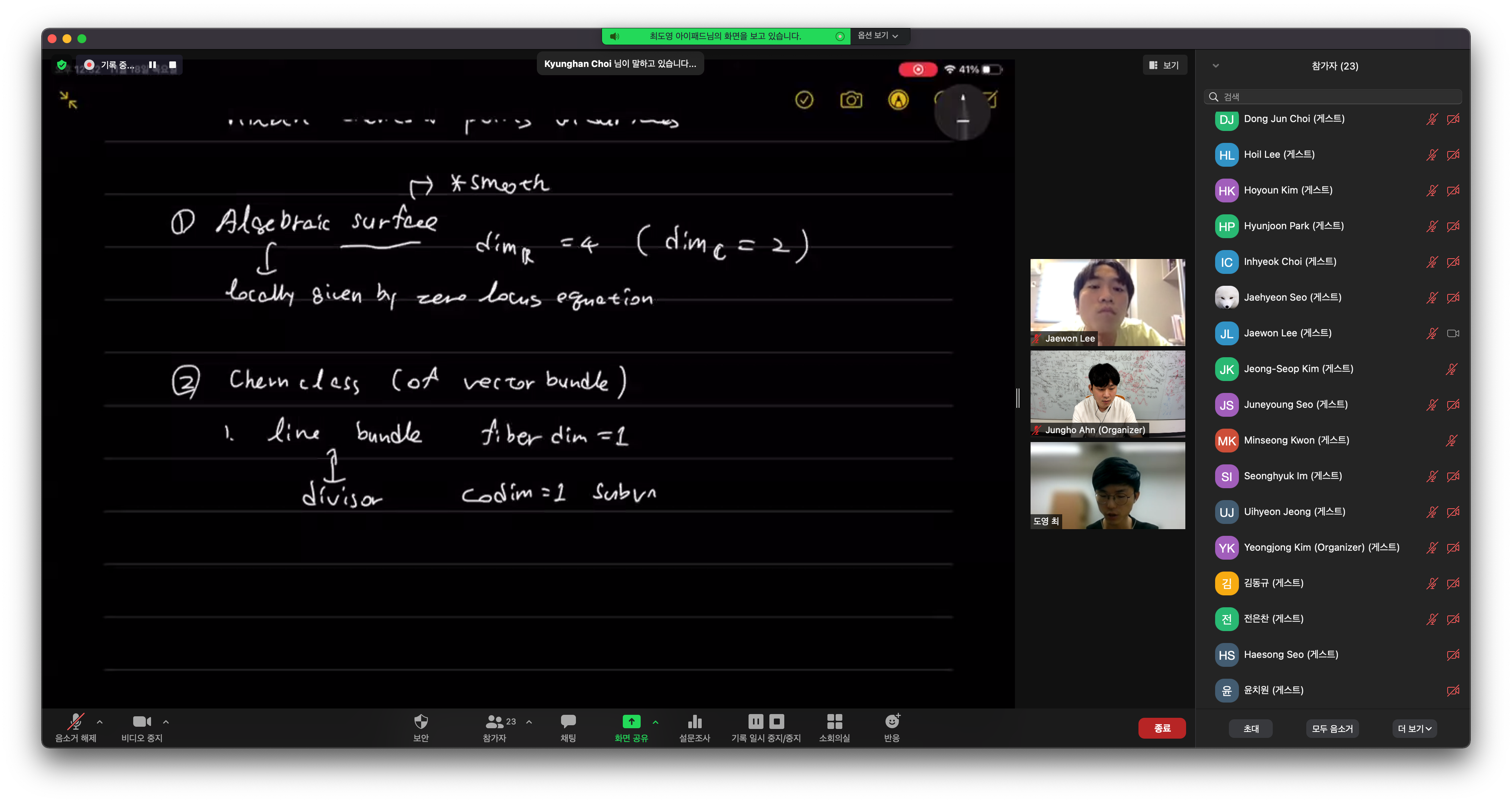
Speaker: Doyoung Choi (최도영) from Dept. of Mathematical Sciences, KAIST and IBS Center for Complex Geometry (CCG), supervised by Prof. Yongnam Lee (이용남 교수님)
Title: Chern classes of tautological sheaves on Hilbert schemes of points on surface
Discipline: Algebraic Geometry
Abstract: I will introduce some concepts of Chern classes, Hilbert schemes and tautological sheaves on Hilbert scheme of points which is associated to a line bundle on surfaces. Also, I will provide a brief description of Lehn’s work which gives an algorithmic approach of the action of the Chern classes of tautological bundles on the cohomology of Hilbert schemes of points on a smooth surface. His work is based on the framework of Nakajima’s oscillator algebra. At the end, I will present the computation of the top Segre classes of tautological bundles associated to line bundles on $Hilb^n$ up to $n \leq 7$, extending computations of Severi, LeBarz, Tikhomirov and Troshina.
Language: Korean