Spectral radius and fractional matchings
in graphs
in graphs
Suil O
Georgia State University
Georgia State University
2014/12/23 Tuesday 4PM-5PM
Room 1409
Room 1409
A fractional matching of a graph G is a function f giving each edge a number between 0 and 1 so that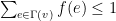 
for each 
, where 
is the set of edges incident to v. The fractional matching number of G, written 
, is the maximum of 
over all fractional matchings f. Let G be an n-vertex graph with minimum degree d, and let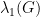 
be the largest eigenvalue of G. In this talk, we prove that if k is a positive integer and ![\lambda_1(G) < d\sqrt{1+\frac{2k}{n-k}}[/latex], then [latex]\alpha'_*(G) > \frac{n-k}{2}](https://s0.wp.com/latex.php?latex=%5Clambda_1%28G%29+%3C+d%5Csqrt%7B1%2B%5Cfrac%7B2k%7D%7Bn-k%7D%7D%26%2391%3B%2Flatex%26%2393%3B%2C+then+%26%2391%3Blatex%26%2393%3B%5Calpha%27_%2A%28G%29+%3E+%5Cfrac%7Bn-k%7D%7B2%7D&bg=ffffff&fg=000000&s=0 "\lambda_1(G) < d\sqrt{1+\frac{2k}{n-k}}[/latex], then [latex]\alpha'_*(G) > \frac{n-k}{2}")
.
for each , where is the set of edges incident to v. The fractional matching number of G, written , is the maximum of over all fractional matchings f. Let G be an n-vertex graph with minimum degree d, and let be the largest eigenvalue of G. In this talk, we prove that if k is a positive integer and .
Tags: 오수일