KAIST Discrete Math Seminar

The choosability of a graph G is the minimum k such that having k colors available at each vertex guarantees a proper coloring. Given a toroidal graph G, it is known that 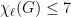, and if and only if G contains . Cai, Wang, and Zhu proved that a toroidal graph G without 7-cycles is 6-choosable, and if and only if G contains . They also prove that a toroidal graph G without 6-cycles is 5-choosable, and conjecture that if and only if G contains . We disprove this conjecture by constructing an infinite family of non-4-colorable toroidal graphs with neither nor cycles of length at least 6; moreover, this family of graphs is embeddable on every surface except the plane and the projective plane. Instead, we prove the following slightly weaker statement suggested by Zhu: toroidal graphs containing neither (a missing one edge) nor 6-cycles are 4-choosable. This is sharp in the sense that forbidding only one of the two structures does not ensure that the graph is 4-choosable.