Finding n such that every transitive permutation group of degree n is multiplicity-free
Mitsugu Hirasaka
Department of Mathematics, Pusan National University, Pusan, Korea
Department of Mathematics, Pusan National University, Pusan, Korea
2009/5/1 Friday 4PM-5PM
This is a joint work with Cai-Heng Li. Let 
denote the set of positive integers n such that each transitive action of degree n is multiplicity-free, and 
denote the set of 
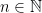such that n=pq for some primes p, q with ![p<q[/latex] and [latex](p,q-1)=1[/latex] where (m,l) is the greatest common divisor of m and n. Our main result shows that [latex]\mathcal{PQ}\backslash \mathcal{MF}[/latex] is the union of <center>[latex]\{pq\in \mathcal{PQ}\mid (p,q-2)=p, q\mbox{ is a Fermat prime}\}](https://s0.wp.com/latex.php?latex=p%3Cq%26%2391%3B%2Flatex%26%2393%3B+and+%26%2391%3Blatex%26%2393%3B%28p%2Cq-1%29%3D1%26%2391%3B%2Flatex%26%2393%3B+where+%28m%2Cl%29+is+the+greatest+common+divisor+of+m+and+n.+Our+main+result+shows+that+%26%2391%3Blatex%26%2393%3B%5Cmathcal%7BPQ%7D%5Cbackslash+%5Cmathcal%7BMF%7D%26%2391%3B%2Flatex%26%2393%3B+is+the+union+of+%3Ccenter%3E%5Blatex%5D%5C%7Bpq%5Cin+%5Cmathcal%7BPQ%7D%5Cmid+%28p%2Cq-2%29%3Dp%2C+q%5Cmbox%7B+is+a+Fermat+prime%7D%5C%7D&bg=ffffff&fg=000000&s=0 "p<q[/latex] and [latex](p,q-1)=1[/latex] where (m,l) is the greatest common divisor of m and n. Our main result shows that [latex]\mathcal{PQ}\backslash \mathcal{MF}[/latex] is the union of <center>[latex]\{pq\in \mathcal{PQ}\mid (p,q-2)=p, q\mbox{ is a Fermat prime}\}")
and 
denote the set of positive integers n such that each transitive action of degree n is multiplicity-free, and denote the set of such that n=pq for some primes p, q with and Tags: MitsuguHirasaka