Injective colorings of graphs with low average degree
Seog-Jin Kim (김석진)
Dept. of Mathematics Education, Konkuk University, Seoul, Korea.
Dept. of Mathematics Education, Konkuk University, Seoul, Korea.
2009/02/27 Fri, 4PM-5PM 3PM-4PM
An injective coloring of a graph G is an assignment of colors to the vertices of G so that any two vertices with a common neighbors receives distinct colors. The injective chromatic number, 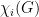 , is the minimum number of colors needed for an injective coloring. Let
, is the minimum number of colors needed for an injective coloring. Let  be the maximum average degree of G. In this paper, we show that
be the maximum average degree of G. In this paper, we show that 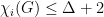 if
if  and
and  . When
. When 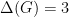 , we show that
, we show that  mad(G) < \frac{36}{13}[/latex] implies [latex]\chi_i(G) \leq 5[/latex]. This is sharp; there is a subcubic graph [latex]H[/latex] such that [latex]mad(H) = \frac{36}{13}[/latex], but [latex]\chi_i(H) = 6[/latex]. This is joint work with Daniel Cranston and Gexin Yu.
mad(G) < \frac{36}{13}[/latex] implies [latex]\chi_i(G) \leq 5[/latex]. This is sharp; there is a subcubic graph [latex]H[/latex] such that [latex]mad(H) = \frac{36}{13}[/latex], but [latex]\chi_i(H) = 6[/latex]. This is joint work with Daniel Cranston and Gexin Yu.
Tags: 김석진