한국 수학사에 큰 획을 그은 최석정(崔錫鼎, 1646~1715)의 직교라틴방진(Orthogonal Latin Squares)과 마방진(魔方陣, Magic Squares)에 관한 짧은 보고와 오늘날도 관심을 가지는 마방진과 관련된 공학/기술적 응용을 살펴보고자 한다.
자연수 n이 주어지면 n차 마방진은 서로 다른 n2개의 숫자가 채워진 n×n 정방의 배열로써 각 행과 열의 합과 두 대각선의 합까지 총 2n+2개의 합이 동일하다는 성질로 정의된다. 여기서 숫자가 1부터 연속적으로 n2까지 사용되면 ‘정규마방진(normal magic square)’이라 한다. 오일러(L. Euler)는 1776년 마방진을 생성하는 다양한 방법에 관한 수학적 이론을 전개하는 논문을 발표했는데, 오늘날 이를 소위 조합수학(Combinatorial Mathematics)의 기원으로 삼는다. 마방진을 생성하는 한 가지 방법이 바로 직교라틴방진을 사용하는 것이고, 몇 가지 조건을 추가로 만족하는 직교라틴방진으로부터 마방진을 생성할 수 있음을 보이면서, 직교라틴방진의 존재와 분류, 생성법 등이 최초로 수학적 이론으로 논의되기 시작했다. 문제는 그 중에서 9차 직교라틴방진이 최석정의 구수략에 표시되었다는 점이다. 최석정이 세상을 떠난 1715년에 구수략이 쓰여졌다고 가정해도 오일러의 논문발표 시점보다 61년 앞서기 때문에 놀라운 사실이 아닐 수 없다.
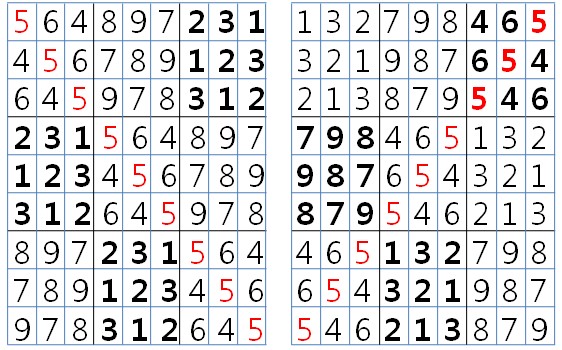
직교라틴방진이란 두 개의 라틴방진을 하나의 방진으로 포갠 후 각 칸에 들어가는 심볼로 순서쌍을 만들었을 때 만들어질 수 있는 모든 순서쌍을 나타낼 수 있는 경우를 말하는데, 그림의 ‘최석정의 9차 직교라틴방진’은 포개었을 때의 순서쌍이 순서대로(5,1), (6,3), …, (5,9)의 81개의 가능한 순서쌍이 모두 나오는 직교라틴방진이다.
공학 분야에서 직교라틴방진 혹은 단순 라틴방진은 여러 가지 쓸모가 많이 있다. n차 라틴방진은 n개의 서로 다른 심볼로 채워진 n×n 정방의 배열로써 모든 행과 열이 이 개의 심볼 각각을 정확히 한 번씩 포함해야 한다. 일반적으로 개의 서로 다른 심볼을 자연수 1부터 n까지 사용하기로 가정하자. 그러면 결국 라틴방진이란 1부터 n까지의 순열(順列, Permutation) n개의 모음이면서 모든 심볼에 대해서 순열마다 그 이미지가 모두 다르다는 특별한 조건이 추가된 모음이다. 더 나아가 매 행에 배열된 심볼의 연속된 순서쌍에 대한 조건을 추가하면서 로만 방진(Roman Squares), 터스칸 방진(Tuscan Squares), 플로렌틴 방진(Florentine Squares), 바티칸 방진(Vatican Squares) 등으로 부르기도 한다. 결국 이러한 방진들은 모두 공통적으로 매우 특별한 조건을 만족하는 개의 순열의 집합이고, 여기서 조건이란 응용분야에 따라서 조금씩 다르지만, 이러한 순열집합은 군통신의 코드 설계분야, 이동통신용 오류정정부호의 스크램블러 설계분야, 더 일반적으로 특수한 임의배열(randomizing) 효과가 필요한 모든 설계분야에 긴요하게 사용되고 있다.
