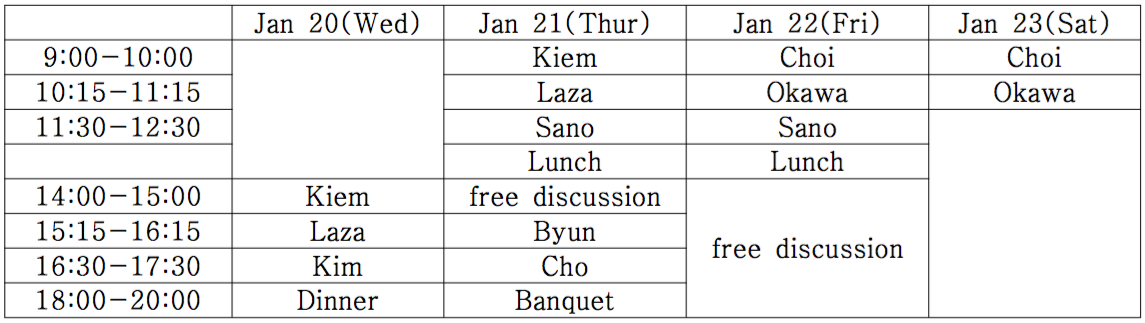
Time Table
Title & Abstract
Jinwon CHOI
Rational curves on del Pezzo surfaces
There are several different ways to count rational curves on a del Pezzo surfaces. In the first talk, I will review some of them. In the second talk, I will discuss a surprising but yet conjectural relationship between two ways of counting rational curves and provide some evidence for it. This is joint ongoing work with Michel van Garrel and Nobuyoshi Takahashi.
Young-Hoon KIEM
Deformation of moduli of vector bundles over curves and Fano visitor problem
The Fano visitor problem asks if the derived category of a smooth projective variety can be embedded into that of a Fano variety. This problem was solved for low genus curves by Kiem-Kim-Lee-Lee. Recently Narasimhan proved that all curves are Fano visitors by using the deformation theory of moduli of vector bundles over a curve. I will talk about Narasimhan's results and generalizations.
Radu LAZA
Birational Geometry of the moduli space of K3 surfaces
The moduli space of polarized K3 surfaces of a given degree d is identified with a locally symmetric variety, and hence has a Baily-Borel compactification. While this compactification is canonical, it has little geometric meaning. Thus, it is of interest to compare it with other more geometric compactification. Specifically, the GIT quotients for m-embedded polarized K3's provide different (projective) birational models of the Baily-Borel compactification. E. Looijenga has constructed a framework that allows to compare these compactifications (for low degree d and m=1). In this talk, I will discuss an enrichment of this picture, essentially a continuous interpolation between the GIT (for all d and m) and BB models. While the discussion will be mostly concerned with the case of hyperelliptic quartic K3 surfaces, we expect such an interpolation to hold quite generally. There is a strong analogy with the Hassett-Keel program that studies the birational geometry of the moduli space of curves. Furthermore, we expect that our work to have applications to the study of asymptotic GIT for K3 surfaces (and be related to the K-stability theory of Donaldson, Tian and others). This is a report on joint work with K. O'Grady.
Shinnosuke OKAWA
Compact moduli spaces of noncommutative del Pezzo surfaces via quivers
An algebraic variety X is recovered from the abelian category of coherent sheaves on X. On the other hand, deformations of the category (= noncommutative deformations of X) are more general than those of X. In the talks, I will explain the deformation theory of abelian categories due to Lowen and Van den Bergh, and introduce certain construction of compact moduli spaces of those categories via quivers. The case of del Pezzo surfaces will be discussed in detail. I would also briefly explain relations to noncommutative projective planes and their blowups in the sense of noncommutative algebraic geometry. My talks are based on joint works in progress with Tarig Abdelgadir and Kazushi Ueda. Part of our results are available in arXiv 1411.7770, 1403.0713, and 1402.3768.
Taro SANO
Deformations of Q-Fano 3-folds
A Q-Fano 3-fold with terminal singularities is a natural object to classify from the viewpoint of MMP. Toward the classification, it is important to consider the deformations. We can deform a 3-fold terminal singularity to quotient singularities and it is called a Q-smoothing. In my talks, I will explain about (1) unobstructedness of deformations and (2) global Q-smoothing of a Q-Fano 3-fold. To show the unobstructedness of deformations, I apply the T^1-lifting method to deformations of a pair. To show the Q-smoothability, I use some Hodge theoretic invariant of a singularity introduced by Namikawa-Steenbrink.
Sangho BYUN
Stability of nets of quadrics in P^5 and associated discriminants
Let S be a complete intersection surface defined by a net N of quadrics in P^5. In this talk we analyze GIT stability of nets of quadrics in P^5 up to projective equivalence and discuss some connections between a net of quadrics and the associated discriminant sextic curve. In particular, we prove that if S is normal and the discriminant of S is stable then N is stable. And we prove that if S has the reduced discriminant and the discriminant is stable then N is stable. Moreover, we prove that if S has simple singularities then the discriminant has simple singularities.
Yonghwa CHO
Establishing exceptional collections of maximal length on Dolgachev surfaces using deformation theory
In recent years, there were a number of approaches to establish exceptional collections on algebraic surfaces of general type. In this talk, I will introduce our recent approach to construct exceptional collections of maximal length on algebraic surfaces with Kodaira dimension one. The main idea is motivated by Hacking's exceptional vector bundle construction, which associates exceptional vector bundles to singular degenerations of underlying surfaces. This is a joint work with Yongnam Lee.
Hosung KIM
The scheme structure of the relative Hilbert scheme of projection morphisms
In this talk, we will show the scheme structure of the relative Hilbert scheme parametrizing the subschemes of the fibers of projection morphisms of hypersurfaces in P^n. To do this we will identify it with the variety of minimal rational curves on a certain Fano manifold. This description allows us to understand the Picard group of the relative Hilbert scheme.