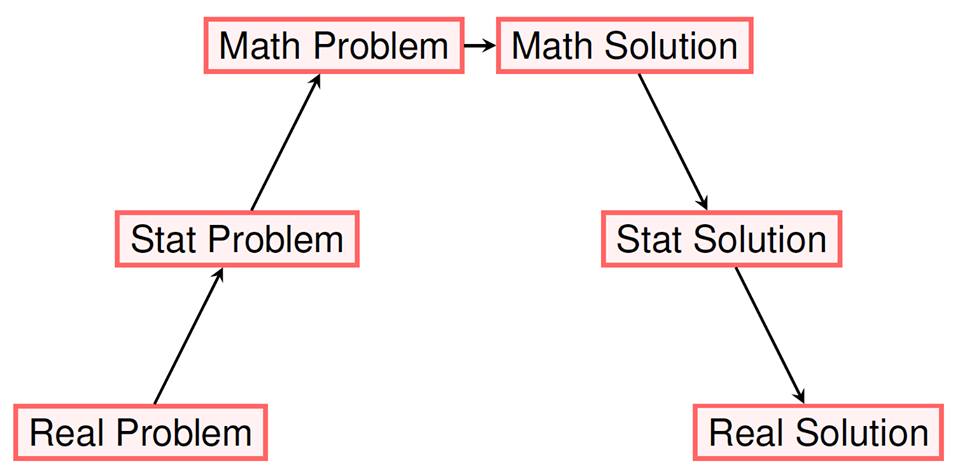
위 그림은 통계학자의 문제해결법을 도식화한 그림입니다. 통계학은 흔히 오차의 과학, 데이터의 과학이라고 하지요. 현상 분석과 예측, 진단, 최적화 등 현실세계에서 발생하는 많은 문제들이 통계학의 문제로 환원되는 경우가 많습니다. 이런 현실 문제는 똑같은 유형으로 발생하는 경우도 있지만 많은 경우 매번 다른 형태의 모습을 가지고 나타나기도 합니다. 여기가 통계학자의 호기심을 자극하는 지점이기도 하지요. 새로운 문제를 푸는 것은 처음 가보는 곳에서 길을 찾는 것과 비슷합니다. 처음 가보는 곳에서 길을 찾는 가장 좋은 방법은 지도를 이용하는 것이겠지만 만약 그곳이 인류 최초로 가보는 곳이라면 이야기가 달라집니다. 그곳에는 지도가 없을 테니까요. 그러면 지도 없이 어떻게 길을 찾을 수 있을까요?
이러한 경우 가장 일반적인 접근법은 산처럼 높은 곳으로 올라가서 아래를 바라보는 것입니다. 높은 곳으로 올라간다는 말은 결국 추상화(또는 단순화)한다는 말입니다. 현실 문제를 풀 때에도 마찬가지 입니다. 통계학자는 높은 곳에 올라가서 통계라는 렌즈로 그 문제를 바라봅니다. 일종의 통계적 “개념화” 작업을 하는 것입니다. 즉, 현실 문제를 통계 언어로 기술하는 것이 통계학자의 첫 번째 작업입니다.
두 번째로는 그렇게 개념화된 통계 문제를 풀어야 합니다. 이를 위해서는 종종 수학적 지식을 가져다가 사용해야 합니다. 전형적인 통계 문제가 아니라 새로운 통계 문제인 경우에는 알려진 해법이 없으므로 이를 해결하기 위해서는 수학이라는 더 높은 산에 올라가서 통계 문제를 수학 문제로 바꾸는 작업을 해야 합니다. (수학이 통계보다 높은 곳에 위치한 이유는 수학이 더 추상적이기 때문입니다.) 통계 문제를 “수학”이라는 렌즈로 바라봄으로써 수학적 해결책을 찾은 후 이를 통계적 해결책으로 번역하면 통계 문제가 해결 되는 것입니다. 이렇게 대부분의 문제 해결의 첫걸음은 단순화에서 시작하는 것입니다.
예를 들어, 2차 세계대전 막바지에서 영국에 대한 독일군의 미사일 무차별 공격이 극심했는데 영국군 당국은 이러한 신무기의 무차별적 폭격을 받는 동안 과연 이 신무기가 어느 정도의 조준 능력을 가지고 발사된 것인지 알아내어야 했습니다. 그래서 영국군은 남부 런던의 피폭격 위치에 대한 정보 데이터를 가지고 보험회사에서 일하는 클라크라는 통계학자의 자문을 받았습니다. 남부 런던에는 537개의 폭격을 맞았는데 그냥 지도상으로 봐서는 그 위치가 우연하게 얻어진 것인지 아니면 어떤 타겟들을 대상으로 했던 것인지 판단하기 어려웠기 때문입니다. 통계학자 클라크 박사는 그 남부지역 144평방 킬로미터 지역을 0.5 킬로미터씩 가로 세로 같은 간격으로 해서 576개의 동일한 크기의 격자로 만든 후 그 격자 안에 몇 번의 폭격이 있었는지를 계산했습니다. 만약 위치가 우연으로 결정된다면 각 격자에서 일어나는 폭격 횟수는 포아송 분포를 따르는 것으로 볼 수 있습니다. 이때 포아송 분포의 모수를 추정하여 각 사건에 대한 기대값을 계산한 후 그것이 실제 발생된 것과 통계적으로 얼마나 차이가 있는지에 대한 카이제곱 검정을 통해서 실시할 수 있었고 그 결과 위치가 우연으로 결정된다는 귀무가설을 기각하지 못하고 영국군은 안심하고 공격에 집중할 수 있었다고 합니다. 이러한 통계 모형의 모수 추정 문제는 수학에서의 최적화 문제로 이해될 수 있습니다.
이런 식으로 단순화를 통해서 문제를 바라보고 사고하는 것은 문제 해결 가능성을 높힐 수 있다는 장점이 있지만 그게 실제와 다를 수 있다는 것도 염두에 두어야만 합니다. 문제를 너무 단순하게 만들면 그게 내 책상 위에서는 풀리겠지만 바깥의 현실 세계와는 괴리가 생길 수 있기 때문입니다. 쌀뜨물을 버리면서 씻은 쌀까지 버리는 오류를 범할 수는 없는 것입니다. 그래서 현실과 이론의 간극을 좁히기 위해서 더 깊이 사고해야 하는 것이 우리 통계학자와 수학자의 과제이고 의무인 것입니다.